Les autres méthodes de positionnement :

Il existe d'autres méthodes de positionnement, utilisant le système GPS. Nous allons en étudier quelques unes.

Le GPS différentiel :

Le GPS différentiel ( DGPS ) fonctionne exactement comme le système décrit précédemment, mais offre des performances nettement supérieures. Le changement s'effectue au niveau du récepteur, qui est équipé d'un boîtier supplémentaire permettant de reçevoir des informations, ou plutôt des corrections en provenance de stations DGPS. En effet, le GPS offre des performances moyennes à cause de la disponibilité sélective (S-A), et dans certaine conditions, la précision peut être réduite à des niveaux inférieurs à ceux d'autres systèmes de radio-navigation à infrastructure terrestre, d'où l'interêt du mode différentiel. Le principe du DGPS est relativement simple ; les mesures effectuées en un lieu de position connue sont comparées aux valeurs théoriques, c'est à dire cartographiques, leur différence fournit alors une correction qui est retransmise vers l'utilisateur, dont le récepteur integrera les corrections dans le calcul de sa position, améliorant considérablement sa précision.

L'application de cette méthode peut se faire à différents niveaux, soit sur la position calculée, soit directement sur la mesure des pseudo-distances. Un récepteur GPS est placé en un lieu de position connue : la station de référence. Ce récepteur reçoit les signaux émis par les satellites et mesure les pseudo-distances. Il les compare ensuite avec les distances théoriques, c'est à dire les distances entre le récepteur et chacun des satellites servant à la mesure de positionnement. La position exacte des satellites est connue grâce à des éphémérides que le récepteur charge en mémoire. Les corrections sont ensuite élaborées et retransmises vers l'utilisateur, via un message connu sous le nom de RTCM SC 104. Le récepteur mobile peut donc appliquer les corrections à ses propres mesures de pseudo-distances. Le DGPS est surtout utilisé à proximité des côtes, et les messages de correction y sont retransmis par les radiophares maritimes sur la bande 285-325 KHz.

La technologie DGPS augmente considérablement la précision la faisant passer de 30 m à moins d'un mètre 50 cm. L'inconvénient d'un tel système est sa portée, qui n'exède pas plusieurs centaines de kilomètres autour des stations d'émmission. Cependant la couverture peut être nettement améliorée grâce à la retransmission des corrections par l'intermédiare de satellites géostationnaires ( WADGPS * ). La couverture est alors étendue à 2000 km, mais les satellites relais sont encore trés peu nombreux.

La mesure de phase* :

1. Principe général

Les récepteurs les plus perfectionnés permettent d'exploiter directement la phase sur les ondes porteuses L1 et L2 en déterminant le déphasage entre le satellite et le récepteur. Le principe de ce système est la comparaison de la phase du signal reçu par le récepteur ( donc émis par le satellite ) avec la phase du signal généré par l'oscillateur à quartz interne au récepteur et qui est une réplique du signal satellite. A partir de cette mesure de phase, on peut obtenir une distance en multipliant par la longueur des ondes porteuses qui est connue : 19,0 cm pour l'onde L1 et 24,4 cm pour l'onde L2. La distance obtenue est la distance satellite-récepteur. Ce mode de mesure est plus compliqué à mettre en œuvre que celui basé sur le code et c'est pourquoi il requiert des récepteurs spécifiques permettant d'exploiter, en plus du code, la phase.
Le traitement des données peut se faire de deux façons : soit en mode post - opératoire à l'aide logiciels spécialisés ; soit en temps réel, au quel cas on parle alors de RTK ( Real Time Kinematic ).

2. Principe physique

En comparant la phase du signal à l'instant de réception ( tR ), à la phase du signal à l'instant d'émission ( tE ), on obtient une différence dØ ( qui est en fait un décalage car l'onde du récepteur est identique à celle du satellite ) qui symbolise le retard de l'onde durant la distance satellite-récepteur avec
delta Ø = Øi(tR) - Øj(tE)

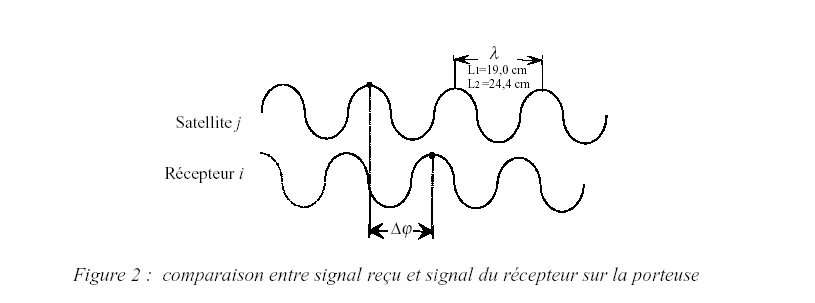
Les Ø représentent les phases du signal du satellite ou du récepteur à un instant t donné. De plus, pour plus de clarté dans ce développement, on apporte l'indice i aux données concernant le récepteur et l'indice j aux données concernant le satellite.

D'autre part, on a la relation générale : Ø(tR) - Ø(tE) = f (tR - tE) (1) où f est la fréquence de l'onde.
D'après la relation v = d / t , on a : t = d / v.
Soit ici comme t = (tR - tE) et v = c où c est la célérité de la lumière dans le vide de 3*10^8 m.s-1
Donc on obtient (tR - tE) = Dij / c où Dij est la distance entre le récepteur i et le satellite j.
En remplaçant dans l'équation (1), on a alors : Ø(tR) - Ø(tE) = Ø(Dij) / c (1')
Lorsque le récepteur compare la phase Øi(tR) de son signal à la phase Øj(tE) du signal qu'il obtient à tR, il obtient un déphasage dØ, compris entre 0 et 1 cycle de phase, c'est-à-dire la partie décimale de la différence Øi(tR) - Øj(tE).
On obtient en fait Øi(tR) - Øj(tE) = dØ(tR) + Nij(tR) (2) où Nij est un nombre entier inconnu de cycles que le récepteur ne peut pas mesurer. C'est-ce qu'on appelle l'ambiguïté initiale.

Ainsi, la première mesure de phase ne détermine en fait que la partie fractionnaire. Ceci est la conséquence du fait que tous les cycles de l'onde porteuse sont absolument identiques, et qu'il est impossible d'identifier un cycle par rapport à un autre.
Mais en plus du déphasage dØ, le récepteur mesure à l'aide d'un compteur le nombre entier de cycles du déphasage reçus depuis la première mesure. Ainsi si t1 est l'instant de la première mesure, pour toutes les autres mesures, on aura, tant que la réception du signal n'est pas interrompue :
Nij(tR) = Nij(t1) + n(tR) où n(tR) est le nombre de cycles comptés par le compteur à l'instant (tR).
On obtient donc en remplaçant dans l'équation (2) :
Øi(tR) - Øj(tE) = dØ(tR) + Nij(t1) + n(tR)
Soit : dØ(tR) = Øi(tR) - Øj(tE) - (Nij(t1) + n(tR))
Par conséquent, pour un satellite donné, la quantité inconnue Nij(t1), qui est le nombre de cycles avant le début du comptage du récepteur, est la même pour toutes les mesures tant qu'il n'y a pas d'interruption du signal. Cette quantité Nij(t1), est appelé ambiguïté entière. On la notera simplement Nij par la suite.

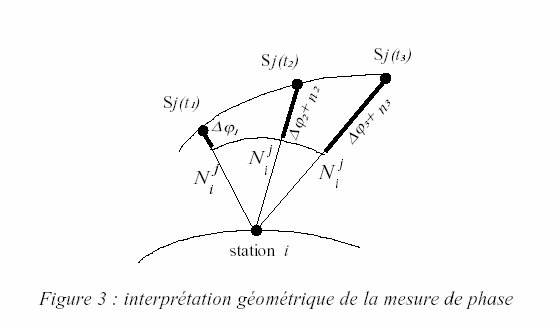
La mesure de phase s'écrit donc :
dØ(tR) + n(tR) = Øi(tR) - Øj(tE) - Nij (3)

De plus, d'après l'équation (1'), on a : Øj(tE) =Øj(tR) - f (Di j) / c
En remplaçant dans (3), on obtient :
dØ(tR) + n(tR) =Øi(tR) - Øj(tR) + f (Di j) / c - Nij
On remarque alors que Øi(tR) - Øj(tR) devrait s'annuler et simplifier cette dernière formule, car le signal délivré par l'oscillateur interne au récepteur est une réplique du signal satellite, soit les ondes du satellite et du récepteur sont identiques, donc les phases des ondes satellite et récepteur devraient être identiques à tout instant t et on devrait avoir : Øi(t) = Øj(t).
Mais cela serait vrai seulement dans un cas fictif, idéal, où les deux horloges seraient parfaitement synchronisées. En réalité il y a un décalage des horloges par rapport au temps GPS. Par conséquent Fi(tR) - Øj(tR) n'est pas tout à fait égal à 0. Ainsi, si Dti et Dtj sont les décalages par rapport au temps GPS (tR), on admettra ici la relation : Øi(tRi) - Øj(tRj) = f (Dtj - Dti)
On peut alors exprimer la mesure de phase en distance en multipliant par la longueur d'onde lambda :
si Ø = dØ(tR) + n(tR)
Ø = f(dtj-dti) + (f*dij)/c - Nij
et d'après la relation sur les ondes c = lambda x f pour les simplifications :
delta Ø = c(dtj-dti) + dij - delta Nij

Mais cette expression n'est pas utilisée ainsi, directement dans les programmes de calculs. En effet la méthode du G.P.S par mesure de phase ne s'utilise que pour le positionnement relatif, ce qui nécéssite pour la mesure une station de référence en plus du récepteur mobile.
De plus on remarque que l'ambiguïté entière est conservée jusque dans l'expression finale et donc qu'il faudra au récepteur la résoudre via des algorithmes qu'il a en mémoire.
D'autre part, une interruption du signal provoque un saut de cycle, c'est-à-dire une autre valeur pour l'ambiguïté qui se traduit par des mesures aberrantes à partir d'un instant donné, qui correspond au saut de cycle, mais qu'on ne connaît pas. La contrainte de ce système par mesure de phase est donc que la liaison satellite-récepteur doit être permanente tout au long de la mesure. De plus un tels système et trés coûteux car il nécéssite un récépteur d'une grande technologie, et la mesure n'est pas instantannée. Ce sont les principales raisons pour lesquelles cette métohde sert principalement aux groupes de scientifiques, avec comme essentielle utilisation, la surveillance de l'évolution des plaques tectoniques ou encore des mesures d'altitude, et d'autres applications ayant attrait à la géologie.

Mesure de phase et fiabilité :

1. Le positionnement relatif par mesures de phase

Avec le positionnement relatif *, on détermine les coordonnées d'un point inconnu (k), à partir des coordonnées d'un point (i) connu à partir de mesures de phases aux deux points i et k, simultanément sur les mêmes satellites.
On a vu précédemment que l'expression de la mesure de phase à la station sur le satellite j est : Mesure de phase et fiabilité :

Ø = f (Dtj-Dti) + ( f x Dij ) / c - Nij
Il existe différents modes de positionnement relatif appliqués à la mesure de phase mais tous sont régis par le même principe de différences afin d'éliminer les erreurs potentielles ; cependant certains sont plus poussés que d'autres dans cette optique et permettent donc d'obtenir des résultats meilleurs.

2.1 La simple différence :

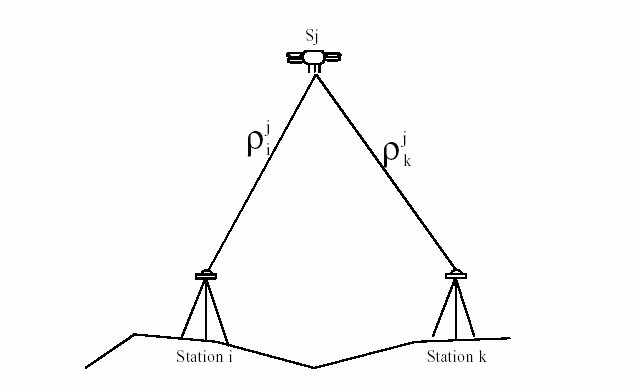
Les stations i et k ( en fait, on a une station fixe au sol, par exemple i, que nécessite le positionnement relatif, et le récepteur mobile, par exemple k) observent le même satellite j au même instant, et on forme la simple différence : Øjik = Øjk - Øji
Soit :Øjik = f(Dti - Dtk) + f(Dkj - Dij)/c - (Nik - Nij)
Le décalage des horloges satellites n'intervient alors plus. C'est l'intérêt de ce principe de mesure. Cependant les horloges des satellites sont des horloges atomiques précises à 10^(-13) secondes près et dont la déviation est régulièrement vérifiée par les stations de contrôle. La déviation qui peut s'opérer par rapport au temps GPS est donc infime. Il serait mieux de parvenir à éliminer le décalage des horloges récepteurs dont le risque de déviation est supérieur.

2.2 La double différence :

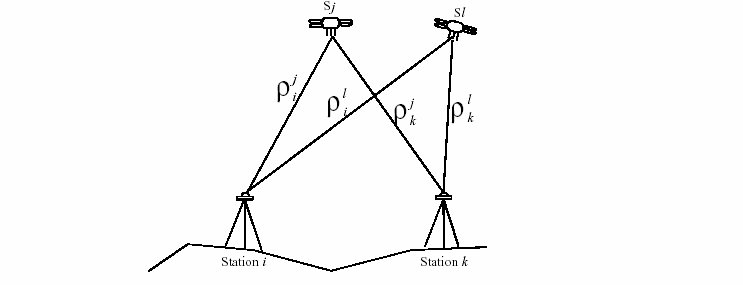
Les deux stations i et k observent les deux satellites j et l simultanément, et on forme la double différence :

Øjl (ik) = Øl (ik) - Øj (ik)
Ce qui donne en remplaçant par l'expression précédente :
Øjl (ik) = f(Dlk - Djk + Dij-Dil) /c - (Nlk - Njk + Nij -Nil)
Ainsi par cette méthode de double différence, le décalage des horloges des récepteurs est alors éliminé. Cependant, le défaut de cette méthode est que, tout comme la précédente, elle conserve les ambiguités entières de la mesure de phase et s'expose donc ainsi aux sauts de cycle.

2.3 La triple différence :

Les stations i et k observent toujours simultanément les satellites j et l, mais en plus, on considère ici les mesures à deux époques tm et tn. On forme alors la triple différence :
Øjl (ik) (nm) = Øl (ik) (n) - Øj (ik) (m)
Øjl (ik) (nm) = f (Dlk(n) - Djk(n) + Dij(n) - Dil(n) - Dlk(m) + Djk(m) - Dij(m) +Dil(m) ) /c
On remarque que, en plus des décalages des horloges satellites et récepteurs, les ambiguités entières sont toute éliminées car l'ambiguîté entière est constante dans le temps tant qu'il n'y a pas d'interruption du signal. En introduisant des variations au cours du temps on peut ainsi l'éliminer. La triple différences est d'ailleurs un moyen de détection des sauts de cycle.

3. Combinaisons de phases et utilisation de la bi-fréquence

Avec des mesures bi-fréquence, c'est à dire en utilisant à la fois les ondes L1 et L2 émises par les satellites, on peut utiliser des combinaisons de phase. Les combinaisons dite " ionosphere-free " et " wide lane " sont les plus répandues .
La combinaison " ionosphere-free " est dite L3 et permet d'éliminer l'erreur ionosphèrique. ( voir partie III )
La combinaison " wide-line " est dite L5 et permet de résoudre plus vite les ambiguïtés.

( lien vers la partie III : la fiabilité du GPS )