Le principe du positionnement
absolu *
:
Le positionnement
par satellite obéit au principe de triangulation. Grâce à
l'horloge atomique que possède chaque satellite, les ondes radio émises
sur L1 et L2 émettent à des instants connus, des signaux codés
selon des fréquences pseudo-aléatoires. Le signal va se propager
ensuite vers le sol, c'est alors que le récepteur va le capter. Afin
qu'un récepteur puisse reconnaître le satellite observé,
chaque satellite transmet un code PRN*
qui lui est propre. Une réplique de la séquence du code du satellite
est générée par le récepteur en même temps
que le satellite. Le décalage que doit subir la réplique afin
de coïncider avec le code reçu correspond au temps de propagation,
pris par le signal, pour parcourir la distance satellite-récepteur. Cette
différence de temps multipliée par la vitesse de la lumière
dans le vide (environ 300 000 km/s) donne une mesure de distance appelée
pseudo-distance ( nous verrons pourquoi plus tard ).
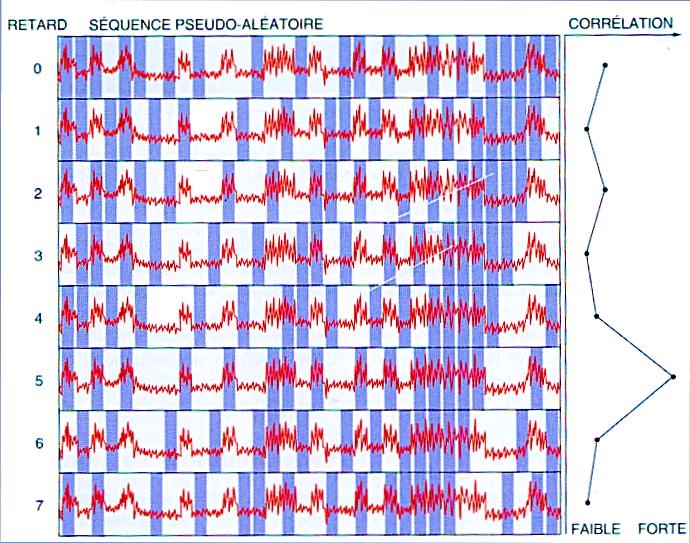
Les taits bleus correspondent à
la réplique du signal du satellite générée par le
récepteur. Le signal rouge correspond au signal émis par le satellite
et reçu par le récepteur. Comme il faut un cetrain temps à
l'onde radio pour parvenir au récepteur, sans appliquer de retard au
signal reçu par le récepteur, les signaux du satellite recus et
ceux générés par le récepteur ne se superposent
pas. Il faut donc chercher le décalage pour lequel il y a correllation
entre les deux signaux, ici il y a correlation pour un décalage de 5,
ce qui correspond en fait à un laps de temps ou retard, c'est à
dire au temps mis par l'onde pour parvenir au récepteur. En multipliant
ce retard par la célérité de l'onde, on obtient la distance
satellite-récepteur.
Plus simplement on peut observer le décalage
suivant entre le signal généré par le satellite et ce lui
reçu par le récepteur , le retard ici observé est de delta
t :

Une seule distance
n'est pas suffisante pour déterminer un point, il faut donc théoriquement,
comme dans le principe d'une triangulation, réaliser la même opération
avec deux autres satellites, portant à trois le nombre de pseudo-distances.
Nous avons donc maintenant trois "pseudo-distances", qui sont inexploitables
si nous ignorons les coordonnées de chaque satellite. Or, le signal émis
par chaque satellite contient un code propre à celui ci, le récepteur
possède les éphémérides des différents satellites
et peut donc obtenir coordonnées de celui-ci au moment de l'émmission
du signal avec une précision de 5 cm. Il ne reste donc plus qu'à
tacer trois sphères dont les centres sont chacun des satellites, de rayon
la "pseudo-distance" séparant le satellite du récepteur,
puis de relever les coordonnées de leur point d'intersection commun,
c'est la position du récepteur.
illustration :

S1
(x, y, z) coordonnées du satellite S1
# S2
(x', y', z') coordonnés du satellite S2 #
S3 (x'',y'',z'') coordonnées du satellite
S3
D1,
distance S1/récepteur
# D2, distance S2/récepteur
# D3, distance
S3/récepteur
Récepteur
: intersections des sphères de centres S1, S2, S3, et respectivement
de rayon D1, D2, D3.
Cependant, ce modèle
appliqué au GPS ne permet pas d'obtenir un point dans un repère
en trois dimensions mais seulement une zone assez vaste, contenant le récepteur.
En effet, les horloges codant le signal au niveau du satellite, sont des horloges
atomiques de trés grande précision, toutes synchronisées
entre elles par les stations de contrôle au sol, et par conséquent
leur dérive n'est que de 10^(-13) secondes par jour. Il en est tout autrement
pour le récepteur, pour des questions de coûts et de technologie,
il est impossible de doter un récepteur d'une horloge atomique, les horloges
utilisées sont donc moins précises, et leur qualité varie
en fonction du modèle employé. Il en résulte que les satellites
et le récepteur ne sont pas parfaitement synchronisés entre eux.
Donc, dans chaque mesure de temps, par la méthode expliquée précédemment,
il réside une erreur infime, mais qui multipliée par la vitesse
de la lumière (pour obtenir la distance), s'amplifie considérablement.
C'est pourquoi le trajet séparant un satellite d'un récepteur
est appelé "pseudo-distance" et non distance, car il n'est
en fait qu'une approximation de la distance réelle. L'astuce à
laquelle ont eut recours les concepteurs du système, a été
de réaliser la mesure de positionnement, non pas avec 3 satellites comme
dans une triangulation classique, mais avec 4 satellites, obtenant ainsi à
coup sûr et malgré les erreurs seulement un point.
Pour obtenir les
coordonnées cartographiques du récepteur, on dispose d'un système
d'équations à 4 inconnues.
( X1 - Ux )²
+ ( Y1- Uy )² + ( Z1- Uz)² = ( D1- dB )²
( X2 - Ux )²
+ ( Y2- Uy )² + ( Z2- Uz)² = ( D2- dB )²
( X3 - Ux )²
+ ( Y3- Uy )² + ( Z3- Uz)² = ( D3- dB )²
( X4 - Ux )²
+ ( Y4- Uy )² + ( Z4- Uz)² = ( D4- dB )²
X,Y,Z représentent
les coordonnées connues des satellites grâce aux éphémérides
( ici respectivement les satellites 1, 2, 3, 4 )
Ux, Uy, Uz, sont
les coordonnées recherchées du récepteur.
( D- dB ) correspond
à la pseudo - distance calculée, où D est la distance réelle
et dB les erreurs dues au système de positionnement.
Connaissant toutes
les variables sauf les coordonnées du récepteur, ont peut déterminer
ces dernières sans difficulté en résolvant le système
d'équations. Le récepteur les traduit alors en latitude et longitude
; l'utilisateur n'a plus qu'à les reporter sur une carte.
Latitude et longitude
:
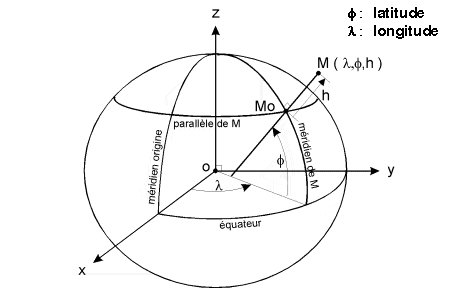
La latitude permet de se repérer
en terme de nord ou de sud , elle s'exprime en degré et correspond à
l'angle que forme la droite joignant le centre de la Terre au point à
positionner avec le plan de l'équateur. Elle varie entre 90° Nord
et 90° Sud.
La longitude permet de se reprérer
en terme d'est ou d'ouest ( avec comme référence le méridien
de Greenwich ) ; elle s'exprime également en degré et correspond
à l'angle que forme le méridien sur lequel se trouve le lieu avec
le méridien de Greenwich. Elle varie entre 180° Ouest et 180°
Est.
Petite
application :
Le GPS donne les
coordonnées du récepteur en longitude et latitude. L'affichage
du récepteur se fait sous la forme de degrés et minutes d'arc.
Exemple N 51°02.327' est une latitude puisque précédée
de N pour Nord ; 51 sont les degrés; 02.327 sont les minutes : 2 minutes
et 327 millièmes de minute. Ce ne sont pas des minutes et des secondes...
Pour la navigation il faut tenir compte de ces millièmes : Dans ce cas,
il valent 600 mètres:
1 minute de latitude correspond à un mille, soit 1852 mètres.
327 millièmes font donc 1,852 x 327 soit: 605,6 mètres.
E 002°22.226' indique une longitude (puisque précédée
par E: Est ou W pour Ouest): 2 degrés, 22,226 minutes de longitude Est.
Mesure de la
vitesse :
Le système
GPS permet également de mesurer la vitesse à laquelle se déplace
l'utilisateur. Cette évaluation se fait par mesure Doppler sur le signal
provenant d'un satellite GPS. En effet, le signal perçu par le récepteur
GPS n'a pas exactement la même fréquence que lorsqu'il est généré
par le satellite. Suivant le principe Doppler, le rapport des fréquences
est fonction des positions et des vitesses relatives du satellite et de l'utilisateur.
En outre, cette mesure permet de détecter et de corriger les sauts de
phase potentiellement présents dans les mesures de phase ( voir partie
II, les autres méthodes de positionnement, la mesure de phase ).

( lien vers la partie II : les autres
méthodes de positionnement )





